2473: 联!合!
题目描述
小A和小B最近迷上了一个益智类游戏,叫“联!合!”。游戏开始,屏幕上会出现一个3*3的网格,每个格子会有不同的底色以及不同颜色的不同图案。我们这里称格子底色、图案形状、图案颜色为该格子的3种属性。小A和小B轮流进行游戏,轮到的人需要在5秒以内说出三个格子,满足这三个格子有两种属性是完全相同的,一种属性是三者各不相同的。例如,下图每个格子按照从左到右从上到下编号。可以是格子底色、图案形状完全相同,而图案颜色各不相同,如下图的1、6、8;也可以是格子底色、图案颜色完全相同,而图案形状各不相同,如下图的1、2、7。
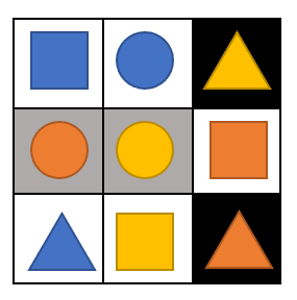
每一轮游戏,轮到的玩家若能找到一组符合要求的之前从未提过的三个格子,则喊出一句“联!”,得一分。若玩家确定再无符合要求的三个格子,则喊出一句“合!”,得两分,从而游戏结束。若玩家未能在规定时间中回答或回答错误,则对方得分。
现在,小A和小B已经把技术练得炉火纯青,现在他们决定把游戏升级。给定一个N行M列的网格,每个格子会有格子底色、图案形状和图案颜色。在最快的时间内,找到所有满足要求的三个格子的组数。然后他们把这个问题交给了你,希望你能给出正确的答案供他们参考。需要注意的是,三个格子的选择顺序调换也算作一种,也就是上述的例子中,1、6、8和6、8、1和1、8、6都是视为同一个选择方案。
输入
第一行包含两个正整数N和M,表示有N行M列。
第二行到N*M+1行,每行包含三个整数,分别为格子底色编号、图案形状编号、图案颜色编号。编号相同则认为属性相同,即若两个格子的底色编号都为1,则认为它们的格子底色是相同的。
输出
样例输入 复制
样例一:
3 3
1 1 1
1 2 1
2 3 2
3 2 3
3 2 2
1 1 3
1 3 1
1 1 2
2 3 3
样例二:
2 4
1 1 2
2 1 1
1 2 1
1 3 1
3 1 1
1 1 3
1 1 1
2 2 2样例输出 复制
样例一:
2
样例二:
3提示
对于40% 的数据,1≤N≤50,1≤M≤50,描述格子的属性编号为不超过5的非负整数。
对于70%的数据,1≤N≤1000,1≤M≤1000,描述格子的属性编号不超过50的非负整数。
对于100%的数据,1≤N≤1000,1≤M≤1000,描述格子的属性编号不超过100000的非负整数。
样例1对应的是上图的情况,其中格子底色编号1、2、3分别对应白色、黑色、灰色,图案形状编号1、2、3分别对应正方形、圆形、三角形,图案颜色编号1、2、3分别对应蓝色、黄色、橙色。存在两组满足要求的三个格子,分别为1、6、8和1、2、7。
样例2存在三组满足要求的三个格子,分别为1、6、7和 2、5、7和3、4、7。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
struct Tpoint {
int t1,t2,t3,id;
};
int N,M,Num;
Tpoint a[1000005];
int third[1000005], num[1000005];
long long C3[1000005],C2[1000005];
bool cmp(Tpoint a,Tpoint b) {
if (a.t1 != b.t1) return a.t1 < b.t1;
if (a.t2 != b.t2) return a.t2 < b.t2;
if (a.t3 != b.t3) return a.t3 < b.t3;
return a.id < b.id;
}
void get_ready() {
for (int i=1; i<=1000000; i++) {
long long t = i;
C3[i] = i*(i-1LL)*(i-2LL)/6LL;
C2[i] = i*(i-1LL)/2LL;
}
}
long long calc() {
long long res = 0;
for (int i=1; i<=Num; i++) {
int j=i;
while (j < Num && a[j+1].t1 == a[i].t1 && a[j+1].t2 == a[i].t2) j++;
int cnt = 0;
third[0] = -1;
num[0] = 0;
for (int k=i; k<=j; k++) {
if (a[k].t3 == third[cnt]) num[cnt]++;
else {
cnt++;
third[cnt] = a[k].t3;
num[cnt] = 1;
}
}
long long total_num = 0;
for (int k=1; k<=cnt; k++) total_num+=num[k];
long long sum = C3[total_num];
for (int k=1; k<=cnt; k++) {
sum-=C3[num[k]];
sum-=C2[num[k]]*(total_num-num[k]);
}
res += sum;
i = j;
}
return res;
}
int main() {
get_ready();
scanf("%d%d",&N,&M);
for (int i=1; i<=N; i++)
for (int j=1; j<=M; j++) {
Num++;
scanf("%d%d%d", &a[Num].t1, &a[Num].t2, &a[Num].t3);
a[Num].id = Num;
}
sort(a+1,a+Num+1,cmp);
long long Ans = calc();
for (int i=1; i<=Num; i++) swap(a[i].t1, a[i].t3);
sort(a+1,a+Num+1,cmp);
Ans += calc();
for (int i=1; i<=Num; i++) swap(a[i].t2, a[i].t3);
sort(a+1,a+Num+1,cmp);
Ans += calc();
cout << Ans << endl;
return 0;
}